Mínimo y Máximo valor de una función
Considere la siguiente notación:
Esta denota el valor mínimo de la función objetivo 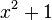 , cuando x se selecciona del conjunto de números reales
, cuando x se selecciona del conjunto de números reales  . El valor mínimo en este caso es
. El valor mínimo en este caso es  y ocurre para
y ocurre para  .
.
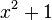 , cuando x se selecciona del conjunto de números reales
, cuando x se selecciona del conjunto de números reales  . El valor mínimo en este caso es
. El valor mínimo en este caso es  y ocurre para
y ocurre para  .
.
De modo similar, la notación
pregunta por el valor máximo de la función objetivo 2x, cuando x puede ser cualquier número real. En este caso, no existe tal máximo si la función objetivo es infinita, luego la respuesta es "infinito"o "indefinido".

No hay comentarios:
Publicar un comentario